EIGamal密码建立在有限域GF(p)的乘法群的离散对数问题的困难性之上。而椭圆曲线密码建立在椭圆曲线解点群的离散对数问题的困难性之上。两者的主要区别是其离散对数问题所依赖的群不同。因此两者有许多相似之处。

1.椭圆曲线解点群上的离散对数问题

椭圆曲线上的解点所构成的交换群恰好是循环群，但是一般并不一定。于是我们希望从中找出一个子群品，而子群E1是循环群。可以证明当循环子群E1的阶lE1l是足够大的素数时，这个循环子群中的离散对数问题是困难的。

设P和Q是椭圆曲线上的两个解点， t为一正整数，旦1≤ t＜|E1l。对于给定的P和t，计算tP=Q是容易的。但若己知P和Q点，要计算出t则是极困难的。这便是椭圆曲线解点群上的离散对数问题，简记为ECDLP(Elliptic Curve Discrete Logarithm Problem) 。

除了几类特殊的椭圆曲线外，对于一般ECDLP目前尚没有找到有效的求解方法。于是可以在这个循环子群E1中建立任何基于离散对数困难性的密码，并称这个密码为椭圆曲线密码。据此，诸如EIGamal密码、Diffie-Hellman密钥分配协议，美国数字签名标准DSS等许多基于离散对数问题的密码体制都可以在椭圆曲线群上实现。我们称这一类椭圆曲线密码为EIGamal型椭圆曲线密码。后来又有人将椭圆曲线密码推广到环Zn上(n=pq)，这类椭圆曲线密码的安全性依赖于对大合数n的因子分解，所以被称为RSA型椭匾曲线密码。于是就有众多的椭圆曲线密码方案。不过，一般谈到椭圆曲线密码大多是指EIGamal型椭圆曲线密码。在这里我们只讨论ELGamal 型椭圆曲线密码。

在SEC1（sec1=1/cos1=无穷大）的椭圆曲线密码标准(草案)中规定，一个椭圆曲线密码由下面的六元组所描述：

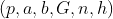
其中，p为大于3 素数， p确定了有限域GF(p)；元素a，b∈GF(p)，a和b确定了椭圆曲线G为循环子群E1的生成元，n为素数且为生成元G的阶，G和n确定了循环子群E1；h=lE1l/n ， 并称为余因子，h将交换群E和循环子群联系起来。

用户的私钥定义为一个随机数d，d∈{1 ， 2,…,n-1} ，用户的公开钥定义为Q点，Q=dG。

2.ELGamal型椭圆曲线密码

为了构建椭圆曲线密码，首先要建立椭圆曲线密码的基础结构，为构造具体的密码体制奠定基础。这里包括选择一个素数p，从而确定有限域GF(p)；选择元素a，b∈GF(p)，从而确定一条GF(p)上的椭圆曲线；选择一个大素数n，并确定一个阶为n的基点。基础参数p，a，b， G，n，h 是公开的。

随机地选择一个整数d，作为私钥。再确定出用户的公开钥Q。

设要加密的明文数据为m，其中0≤m<n 。设用户A要将数据m加密发送给用户B，其加解密过程如下：

加密过程：

①用户A去查公钥库PKDB，查到用户B的公开密钥QB 。

②用户A选择一个随机数k， 且k∈{1, 2,…, n-1} 。

③用户A计算点X1：(x1,y1)=kG。

④用户A计算点X2：(x2,y2)=kQB，如果分量x2=O，则转②。

⑤用户A计算C=mx2 mod n。

⑥用户A发送加密数据(X1，C) 给用户B。

解密过程：

①用户B用自己的私钥dB求出点X2：

dBX1=dB(KG)=k(dBG)=KQB=X2：(x2，y2)。

②求出分量巧的逆x2-1。

③对C解密，得到明文数据m=Cx2-1 mod n。

类似地，可以构成其他椭圆曲线密码。

与EIGamal密码一样，为了安全，加密所使用的k必须是一次性的。这是因为，如果使用的k不是一次性的，时间长了就可能被攻击者获得。又因QB是公开密钥，攻击者自然知道。于是攻击者就可以计算出点X2，获得分量足，进而求出X2-1。又因为攻击者可以获得密文C，于是可以计算CX2-1 mod n得到明文m。

同样，解密钥d选得太小或太大都不好。因为攻击者在用穷举方法猜测d时，一般会首先试验太小或太大的d。同理，随机数k也不要选得太小或太大。随机数k的选择还要保证点X2的分量X2 mod n≠1。如果X2 mod n =1，则会使密文C=m X2=m mod n，从而暴露明文m。