拟合是数学和统计学中的一个重要概念，指的是通过建立一个数学模型来尽可能准确地描述观测数据中变量之间的关系，使得模型能够最好地匹配给定的数据集。这个过程也被称为曲线拟合或参数估计，目的是找到一个能够最好地解释或预测数据点的模型，以便对新的、未见过的数据进行推断或预测。
一、拟合的类型
- 线性拟合：当待定函数是线性时，称为线性拟合。
- 非线性拟合：当待定函数是非线性时，称为非线性拟合。
- 样条插值：表达式可以是分段函数时，称为样条插值。
二、拟合的应用场景
在机器学习中，拟合通过训练数据来调整模型参数，使得模型输出接近真实数据。拟合程度决定了模型的表现，主要分为三种情况：欠拟合、适度拟合和过拟合。
欠拟合：模型过于简单，无法捕捉数据中的模式和复杂关系，导致训练误差较大。
适度拟合：模型能够很好地捕捉数据的模式，训练误差和测试误差都较小，具有良好的泛化能力。
过拟合：模型过于复杂，捕捉到了数据中的噪声和细节，导致训练误差较小但测试误差较大。
三、拟合的数学原理
拟合也是用有限的数据点构造近似函数的一种方法，但拟合不要求拟合函数一定要过数据点，使总偏差达到最小即可(比如高斯的最小二乘回归)，拟合函数反映对象整体的变化态势。
具体来说，就是给定一系列离散的数据点：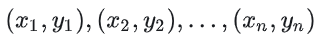
，我们要找到一个函数f(x)，使 f(x) 在某种准则下与所有数据点最为接近。
令
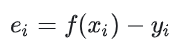
ei为第 i 点拟合函数值（预测值）与观测值之间的差，称为残差。 要使拟合函数尽量接近所有数据点，采用残差的最小平方和为评价标准，即：
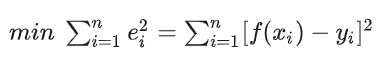
这也是我们熟悉的最小二乘原则，最小二乘原则确定拟合函数的方法称为最小二乘法。
一般来说，拟合函数使自变量 x 和待定系数 a1,a2,...,am 的函数
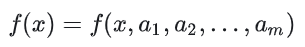
根据参数 a1,a2,...,am 线性与否，将最小二乘法分为线性最小二乘法和非线性最小二乘法两类。
四、拟合函数选择
数据拟合时，首要也是最关键的一步就是选取恰当的拟合函数。如果能够根据问题的背景通过机理分析得到变量之间的函数关系，那么只需估计相应的参数即可。但很多情况下，问题的机理并不清楚。此时，一个较为自然的方法是先做出数据的散点图，从直观上判断应选用什么样的拟合函数。
一般来说，数据分布接近直线，采用线性函数拟合，抛物线则采用二次多项式，如果数据分布特点是开始上升较快随后逐渐变缓，则宜选用双曲线型函数或指数型函数，常被选用的拟合函数有对数函数 y=a1+a2lnx ,S形曲线函数 y=1/(a+be−x )等。
参考资料：
